Abstract
Differentiable Multi-Sensor Kalman Filter for 3D MultiObject Cooperative Tracking (DMSTrack) is a 3D multi‐object cooperative tracking framework for autonomous driving that uses a differentiable multi‐sensor Kalman filter to learn per‐detection measurement uncertainties and fully leverage the Kalman filter’s theoretical strengths. In this work, we evaluate the learnable observation covariance module of DMSTrack, focusing on AMOTA, the primary metric in their work. We show that squaring residuals masks negative covariance adjustments, limiting adaptability and reducing stability. To address this, we introduce a terminal ReLU on the residual network and lower the initial covariance diagonal. Our modifications surpassed the original paper’s best-reported AMOTA, reduced training time required, and mitigated instability, proven by training and validation loss curves. Other variants investigated includes implementing Leaky ReLU or constant covariance with distance-dependent scaling produce performance gains comparable to the original baseline architecture.
Introduction
Autonomous vehicles typically rely on each car’s on‐board sensors for 3D detection and tracking, but single‐sensor pipelines falter under occlusions or sensor failures. While cooperative perception—via early, intermediate, or late fusion—has advanced multi‐vehicle detection, cooperative tracking remains underexplored: even V2V4Real’s [2] benchmark still feeds detections into a standard single‐sensor Kalman filter with fixed noise assumptions, failing to capture cross‐vehicle measurement uncertainty.
DMSTrack [1] bridges this gap by embedding a differentiable multi‐sensor Kalman filter that learns per‐detection observation covariances, thus restoring the theoretical optimality of KF‐based tracking. This approach delivers a 17% relative AMOTA boost over feature‐map fusion methods while using only 3.7% of the communication cost compared to other state-of-the-art methods.However, DMSTrack’s practice of squaring covariance residuals conceals negative corrections, driving unstable convergence and over 30 hours of training time for 20 epochs on an AWS g6.xlarge instance. We tackle these issues with two minimal changes—applying a terminal ReLU to enforce nonnegative residuals and tuning the initial covariance scale—enabling us to reach the original AMOTA in just four epochs (an 80% reduction in training time) and to produce markedly smoother validation loss curves.The key contributions are as follows:
- Re-implementation and comparison of parameter-dependent, learnable covariance residual networks versus fixed covariance tuning in the differentiable multi-sensor Kalman filter.
- Identification and analysis of design limitations in the original learnable covariance residual networks proposed in DMSTrack, specifically, masking negative adjustments due to square residuals.
- Architectural modifications enforcing non-negative residuals (terminal ReLU) and lower initial covariance.
- Performance demonstration showing > 43.61% in the primary metric AMOTA (Average Multi-Object Tracking Accuracy) after 4 epochs, an 80% reduction in training epochs needed across 9 V2V4Real benchmark sequences.
- Additional analysis of a few other directions that we have explored, including constant covariance with distance-dependent scaling and Leaky ReLU–based residuals.
Background
Generally, given CAVs collaboratively tracking objects in 3D space over discrete time steps , each object’s true state is:
where is the object center, its yaw, its dimensions, and its velocity. At each time , CAV produces at most one detection per object:
Under a linear Gaussian model, the state evolves via:
And each detection satisfies:
The goal is to compute the minimum-mean-square-error estimate via sequential Kalman updates across all CAV detections.
DMSTrack [1] formulates 3D multi-object cooperative tracking as an end-to-end differentiable Kalman filter over sensor inputs. After prediction:
it executes sequential measurement updates. Instead of fixed observation noise, DMSTrack learns per-detection covariances:
where concatenates local bird’s-eye-view and positional features, and .
The Kalman update steps are:
The full prediction–update sequence is differentiable, so is trained by minimizing the tracking error over ground-truth trajectories.
DMSTrack constructs the input feature vector by concatenating:
- Local BEV features: cropped and pooled from a PointPillar backbone at two resolutions.
- Positional features: raw box parameters and ego-vehicle transform, then linearly embedded.
These are fused and passed through a two-layer MLP with ReLU activations to predict . The residuals are squared and added to to yield .
DMSTrack is trained on sequences of length . For each time step , tracks within 2m of ground truth incur an L2 loss on the first 7 state variables:
Methodology
Key Findings
Through detailed analysis, we discovered that several residual entries fell within the problematic range of -6 to -5. This led to an important insight: while the model attempts to minimize covariance by generating negative residuals, the formulation of the residual calculation introduces non-smoothness into the loss:
Solution Implementation
To address this, we experimented with constraining to prevent it from crossing zero. The most effective solution was adding a ReLUactivation at the output layer of the covariance residual network. This change significantly improved both the negative log-likelihood (NLL) loss and AMOTA on validation sequences.
Alternative Approaches Explored
We also investigated several alternative approaches:
- Heuristic-Based Covariance Modeling: Instead of learning measurement noise covariance via a neural network, we tested handcrafted heuristics to scale or shape the covariance matrix:
- Scaling covariance based on the detected vehicle`'s distance to the ego car
- Varying covariance based on the detection's map location
However, we quickly realized that these heuristics were manually approximating functions that the network could learn more robustly using the same feature set.
- LeakyReLU Activation: Since , we also explored LeakyReLU (slope = 0.05) to allow slightly negative residuals while biasing toward positive values. Although theoretically sound, this approach underperformed compared to a simple ReLU activation.
Experimental Results
Dataset, Training Process, and Evaluation Metrics
Dataset
To ensure a fair comparison with DMSTrack, we adopt the same data pipeline on V2V4Real, a real-world multi-agent cooperative perception dataset. We use only LiDAR point clouds and 3D bounding box ground truths:
- Training: 32 sequences, 7105 frames
- Validation: 9 sequences, 1993 frames
Training Procedure
We compare four variants—original DMSTrack, a constant-covariance baseline, and our two modified versions (terminal ReLU and terminal Leaky ReLU)—under the same regimen on V2V4Real for fairness. Each uses a two-CAV ObservationCovarianceNet (fusion features, ) and is trained end-to-end with Adam (lr = , wd = ), gradient-norm clipping at 1. We process full sequences (no sub-splits), back-propagate every 10 frames on only the regression loss (weight = 1), and zero out association and NLL losses. After evaluation at epoch 0, we validate—and log AMOTA, sAMOTA, AMOTP—at each epoch’s end.
The ReLU variant runs for 8 epochs; Leaky-ReLU and original DMSTrack run for 20, selecting the best checkpoint by validation. For the constant-covariance baseline, we fix and (AB3DMOT [3] defaults) and simply evaluate without learning.
Evaluation Criteria
Quantitative Metrics: As defined in DMSTrack and V2V4Real:
- AMOTA: average multi-object tracking accuracy over a range of recall thresholds (higher is better)
- AMOTP: average localization precision of matched tracks (higher is better)
- sAMOTA: AMOTA scaled by the number of objects to correct for varying sequence difficulty (higher is better)
- MOTA: overall multi-object tracking accuracy with false positives/negatives & ID switches (higher is better)
- MT: fraction of ground-truth trajectories that are tracked for at least 80 % of their length (higher is better)
- ML: fraction of ground-truth trajectories that are tracked for at most 20 % of their length (lower is better)
Training & Validation Losses:
- Regression Loss:
- Negative Log-Likelihood (NLL) Loss:
Qualitative Evaluation: Open3D visualizations show ground truth (green), raw detections (yellow/blue), and fused tracks (red).
Training and Validation Losses Performance Analysis
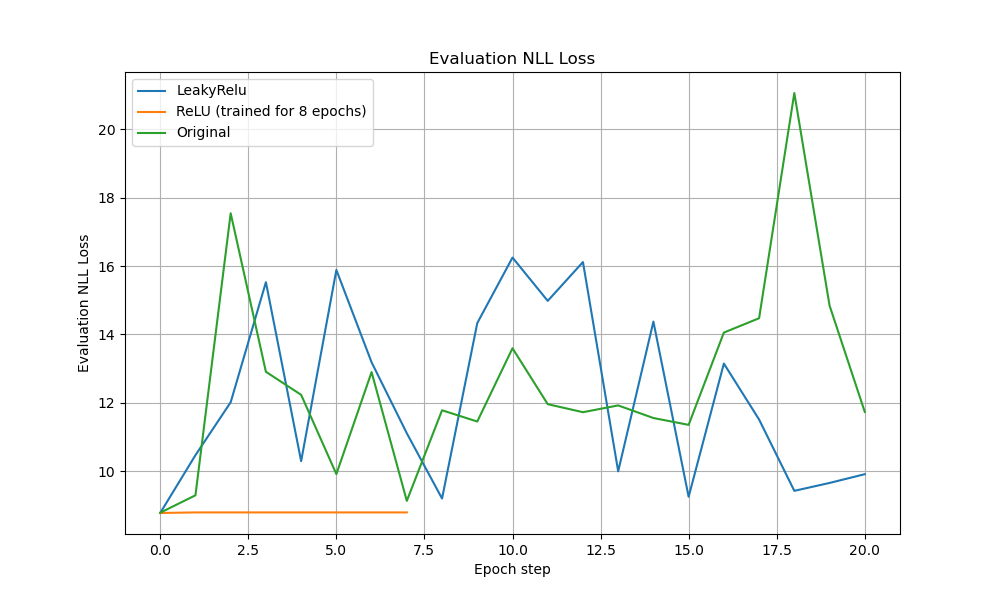
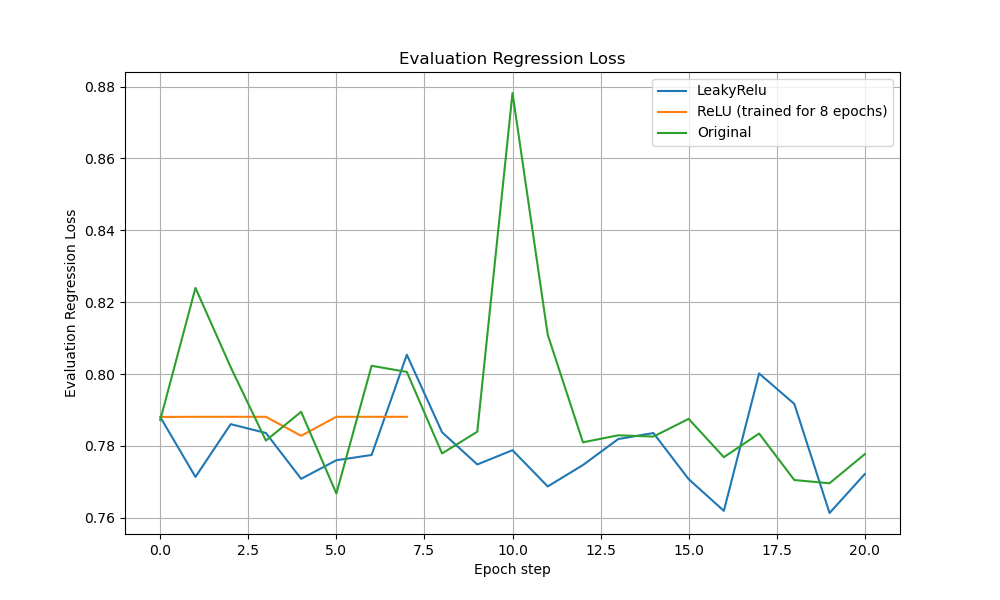
The ReLU model showed flatter, lower training losses throughout. Validation loss curves confirmed ReLU’s stability, outperforming LeakyReLU and original DMSTrack across both NLL and regression metrics.
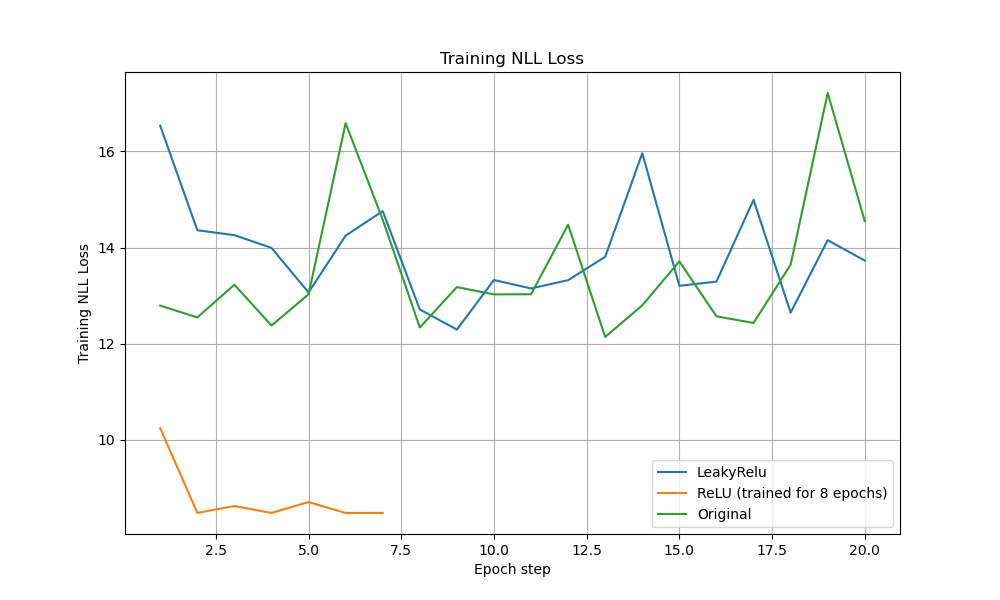
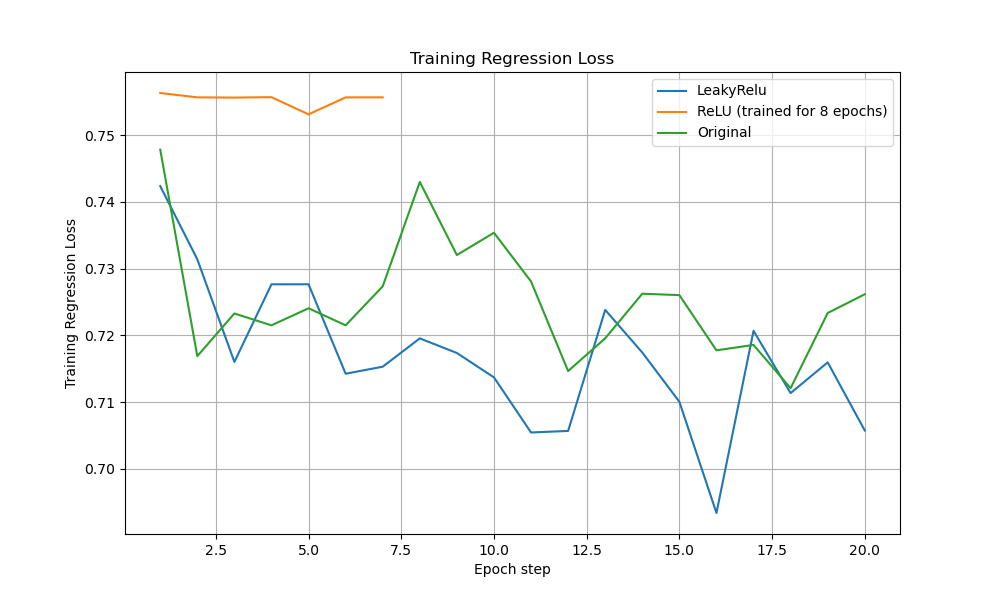
During training, the ReLU-clamped model achieves dramatically lower and flatter losses: its negative log-likelihood stays near 8.5–9.0 throughout all 20 epochs (versus 12–16 for LeakyReLU and 12–17 for the original DMSTrack), and its regression loss remains tightly grouped around 0.75–0.76 (versus 0.70–0.75 for LeakyReLU and 0.72–0.75 for the original DMSTrack). This stability stems from ReLU’s strict non-negativity on the covariance residuals, which prevents invalid negative-variance gradients and yields a smoother, more reliable optimization trajectory.
On the validation set, the benefits of hard clamping are even clearer: the ReLU model’s NLL loss is a flat line at , while LeakyReLU fluctuates between 9 and 16 and the original DMSTrack occasionally spikes up to 21; similarly, ReLU’s regression loss remains constant at, whereas LeakyReLU and the original DMSTrack oscillate between 0.77–0.80 and briefly peak at 0.88. In effect, ReLU’s enforcement of positive-definiteness delivers both lower error and far less variance in performance, highlighting why LeakyReLU, by permitting small negative residuals, fails to converge as cleanly.
V2V4Real Tracking Metrics
The final evaluation metrics across all model variants are summarized below:
| Method | AMOTA ↑ | AMOTP ↑ | sAMOTA ↑ | MOTA ↑ | MT ↑ | ML ↓ |
|---|---|---|---|---|---|---|
| Constant Covariance | 41.51 | 55.87 | 89.37 | 88.68 | 66.67 | 13.67 |
| Default DMSTrack | 43.52 | 57.94 | 91.50 | 88.32 | 68.35 | 13.19 |
| DMSTrack + ReLU (Ours) | 43.61 | 57.51 | 91.64 | 88.71 | 67.39 | 13.43 |
| DMSTrack + Leaky ReLU (Ours) | 41.48 | 54.83 | 88.92 | 88.10 | 66.43 | 13.43 |
On the primary DMSTrack metric of AMOTA, our ReLU-enhanced variant achieves 43.61%, noticeably outperforming the constant-covariance baseline (41.51%) and slightly surpassing the original DMSTrack (43.52%). It also leads in sAMOTA and MOTA, while delivering competitive results across all other supplementary metrics. These findings reinforce the effectiveness of our residual-clamping strategy, which not only improves tracking accuracy but also significantly reduces training complexity and instability.
Qualitative Tracking Results
See full video: https://youtu.be/iMu7Uq024Tg

Observing the central objects across these consecutive frames, our filter consistently leans toward the more confident measurement. Instead of averaging the detections equally, the final fused track (red) remains closer to the sensor’s box (yellow or blue) that is either spatially nearer to the ground truth (green) or exhibits higher reliability. This behavior emerges naturally from the learned observation covariance: the model inflates for uncertain detections—such as occluded or distant objects—and shrinks it for clearer views, enabling adaptive, smooth tracking. As the video demonstrates, this strategy maintains robust track continuity even when one CAV’s raw input temporarily degrades.
Conclusion
Our experiments demonstrate that a minimal modification—enforcing nonnegative covariance residuals via a terminal ReLU combined with a reduced initial scale—yields significant benefits in cooperative 3D tracking. By clamping residuals to zero, we eliminate invalid negative-variance gradients, resulting in dramatically smoother training and validation losses, an 80% reduction in training time, and a clear AMOTA improvement over the original DMSTrack. Neither constant-covariance nor LeakyReLU variants achieve this same stability–accuracy trade-off, underscoring the importance of sign-consistent uncertainty learning.
By revisiting classic multi-sensor Kalman filters and recent differentiable KF formulations, we show that simple architectural adjustments can restore theoretical guarantees in end-to-end deep systems. Unlike prior cooperative trackers that rely on fixed noise assumptions or heavyweight fusion networks, our ReLU-clamped DMSTrack achieves near-optimal measurement fusion with minimal inter-vehicle communication, while also delivering much faster and more stable training—making it both more reliable and easier to adopt at scale.
Looking forward, scaling to larger fleets or denser environments will require innovations such as more efficient update schedules, hierarchical filter architectures, or asynchronous fusion schemes. Addressing these challenges is essential for enabling truly resilient cooperative tracking in real-world autonomous driving deployments.
References
[1] Chiu et al. (2024).DMSTrack: Differentiable Multi-Sensor Kalman Filter for 3D Multi-Object Cooperative Tracking. arXiv:2309.14655.
[2] Xu et al. (2022).V2V4Real: A Real-World Large-Scale Multi-Vehicle Cooperative Perception Dataset. arXiv:2303.07601.
[3] Weng et al. (2020).AB3DMOT: A Baseline for 3D Multi-Object Tracking and New Evaluation Metrics. arXiv:2008.08063.
